
In PART I of this series we discussed how to approach Abstract Reasoning Test questions. In PART II we look at simple rules that are relatively easy to spot and won’t make you go cross-eyed staring at the screen. Clear your mind, focus and file away in your memory these common rules used by abstract reasoning question writers. Then when you attempt your next abstract reasoning practice test, try to apply these newly acquired insights.
Rules that are “easy for the eyes”
Once you have completed many sample abstract reasoning questions, you will start to recognise common and reoccurring elements. Some of these elements become easier to spot after a while, as they are not overly confusing and easier for your eyes to recognise. Let’s take a look at some of these rules.
Increasing/Decreasing Numbers
You will encounter many variations of this rule. For example, the number of overlaps between different building blocks may increase/decrease, or the number of sides a shape has may decrease/increase, or the number of icons/items featured may increase/decrease throughout the series. In the example below, you can see that the number of sides a shape has, increases throughout the series. Therefore, the next image block in the series will need to feature a shape with eight sides.

Changing Shapes/Icons
Sometimes shapes or icons will change, because another building block or rule dictates that it does so. In the series above, the shape featured in each image block changes throughout the series because the rule states that the number of sides increases each step. In other cases, the shapes/icons may seem to change randomly, but from the first four image blocks of the series, you will generally be able to tell what will logically come next. In the series below, you can see that the icon to feature in the sixth image block will be a heart, because the icon only appears twice in the series before it changes to a differently shaped icon.
![]()
Fill & Shading
Over the series you may notice that one (or more) of the building blocks change colour – possibly alternating between black, grey, white or different patterns. This is the case in the series above, where you have an alternating patter of an icon being coloured and then uncoloured. Alternatively, the direction/the way the pattern is drawn may also change throughout the series – so keep a close eye out for that. In the image below, you can see the line pattern is rotating in a clockwise direction throughout the series. The next image block in the series will therefore feature a shape with vertical lines. Later when we talk about more complex rules, you will find that sometimes one building block may even affect another building block’s colour/appearance. This was briefly touched upon in Part I of this series, were we talked about “Building block(s) in the series change as a result of an interaction”.

Movement & Position Changes
Often you will find that one of the building blocks will move positions throughout the series according to a set rule. This can happen in a variety of ways. A building block may travel slowly in a clockwise/anticlockwise direction throughout the series. This is the case in the series above, where the shapes move in an anticlockwise direction around the image block throughout the series. A building block may move horizontally / vertically / diagonally / backwards / forwards. It may move to a position previously occupied by another icon or to a position where an arrow has pointed to. Sometimes items move within a grid structure or may even exit an image block altogether, only to reappear again later in the series. The possibilities and combinations are endless. In the series below, you can see that the circle moves vertically from the bottom of an image block to the top throughout the series.

Rotation
In addition to building blocks moving to different positions throughout the series, a building block may also rotate in a clockwise/anticlockwise direction. In the series below, we can see that the triangle rotates 90 degrees in a clockwise direction every step of the series. Keep in mind though, that the amount a building block rotates may not stay consistently the same throughout the series. For example, it may rotate 90 degrees first, then 180 degrees the next step, 270 degrees the step after etc…increasing the rotation by an additional 90 degrees each step of the series.

Shaded Areas & Size Changes
In such cases, two different variations in size are possible. The area that is shaded, of a particular building block, can either increase/decrease throughout the series. Alternately, the physical size of the building block could increase/decrease throughout the series. In the image below, you can see both of these changes occurring. The size of the circle increases throughout the series, while the shaded area decreases by 45 degrees every step. In more complex questions the size of an icon/shape or how much of an area is shaded could be affected by the behaviour of another building block or rule.

Alternation
Otherwise known as “every other step”. Keep in mind that a building block might not move in every step of the series – it could move only every second or third step. In the image below the circle moves very slowly, vertically from top to bottom in the series, but only moves to the new position ever other step.

Reflection
In short - a mirror image of what came previously. While in some cases reflections are easy to spot, this type of rule can be manipulated in a number of ways to make it far more harder to notice. Usually we see that image blocks 1&2, 3&4, 5&6 in the series are reflections of each other – as you can see in the example below. Test writers also like to use abstract forms when engaging reflection as a rule, because it is easier to get confused. The trickiest type of reflection to see however, is when a symmetrical object is involved, as they are always reflected into their original form - such as a circle. It is important to note that the position of the mirror may also change throughout the series. The mirror may be positioned vertically, horizontally or even diagonally. For example, in the series below we can see that image block 2 is a vertical reflection of image block 1, but image block 3 is a horizontal reflection of image block 2, while image block 4 is again a vertical reflection of image block 3 – the position of the mirror alternates between vertical and horizontal throughout the series.

Grid Positioning
As mentioned earlier under “Movement and Position Changes”, building blocks can move within a grid structure in a number of ways. The different rows or columns of a grid may be influenced by different rules and function independently, or the grid may be influenced as a whole by specific rules. Some possible rules influencing a grid could be:
-
Reset: where the building block returns to an original position when it reaches the edge of the grid. In the example below, we can see that the first column follows this rule – the coloured block moves down the column through position 4, 5, 6 and then returns to its original position (position 4) when it reaches the bottom of the grid and starts the sequence again.
-
Reverse: where the building block backtracks on the same path when it reaches the edge of the grid. In the example below, we can see that the second column follows this rule – the coloured block moves down the column through position 4, 5, 6. When it reaches the edge of the grid it starts traveling back again through position 5, 4, and will continue on to position 3, 2, 1 in subsequent steps in the series, before starting the journey back down the column again.
-
Repeat: where the building block continues moving in the same direction and on the same path even when it reaches the edge of the grid. In the example below, we can see that the third column follows this rule – the coloured block moves down the column through position 4, 5, 6. When it reaches the edge of the grid it jumps to the very top and stars moving down the column again.
-
In addition to these more obvious grid rules, there are multiple other possibilities, such as elements moving in a zig-zag through the grid, following the grid’s parameter in a clockwise/anticlockwise direction, travelling diagonally, moving to a new position only ever other step…again, the possibilities are vast.

Distractors
Sometimes you will meet an abstract reasoning question that includes a building block that moves/behaves in a random manner with no logical rule attached to it. These evil little obstacles are simply distractors, designed to waste time. If you find yourself completely stumped by a building block in a series, don’t waste your precious time on it! You may be inadvertently trying to solve a distractor, which has no solution. Move on to the other building blocks in the series and try to find the rules governing them. This can produce two favourable outcomes. Firstly, you may successfully arrive at an answer option - revealing that the building block was in fact a distractor and is irrelevant. Secondly, by solving some of the other rules, it may reveal a rule associated with the building block you initially couldn’t solve or at least allow you to make a more educated guess from fewer answer options. Below is a very simplified example. The star randomly rotates and moves within each image block. Its existence in the series is irrelevant. The only logical rule present, is simply that the circle increases in size through the series. A good article which expands on this topic is: Abstract Reasoning: Visual Overload

Accumulation
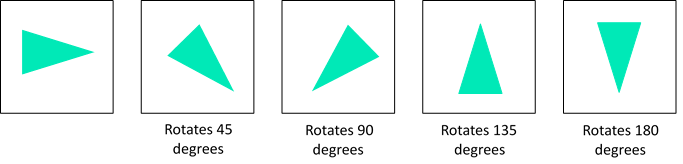
This refers to a rule that makes a building block increase the number of steps it takes or how much it rotates each step of the series. In the example below, we can see that the triangle rotates an extra 45 degrees each step in the series. Another example of this type of rule could be that the number of steps a building block takes, increase in each image as it moves around a grid. The point is that the rotation or number of steps does not stay constant, it increased/decreases throughout the series.
Repeating Patterns
A building block can repeat its movement very regularly (simply jumping back and forth between two positions throughout the series) or only repeat after the third or fourth step of the series (as seen in the example under “Movement & Position Changes”). The less a pattern repeats the harder it is to spot. In the example below, the heart jumps between three positions, following a triangular path from the bottom left position, to the middle top, down to the to the bottom right position, before repeating the sequence again throughout the series.

Overlapping
It is possible that you will encounter a situation, where the building block being observed cannot be seen at times. This is due to it being concealed by another building block. In the example below the bar moves right to left throughout the series taking one step each time. The star always moves in a right direction one step each time. In image block 3, the bar and start occupy the same position. We know that the start is still there, but we can’t see it because it is momentarily being concealed by the bar.

Now that you have memories these 13 simple rules try to identify them the text time you do an abstract reasoning practice test. By being more aware of the possible rules used by question writers, you’ll start to solve abstract reasoning questions faster – leaving you more time to work on harder, more confusing questions. Remember, your goal is to correctly answer as many abstract reasoning questions as possible, and time efficiency here is key!
In Part III of “Secrets” To EPSO Abstract Reasoning Success we will expand our knowledge and explore the more complex rules employed by abstract reasoning question writers.
